2025.09.12

【Python】数式計算ライブラリSymPyチュートリアル【微分方程式を解く】

えりる

記事内に商品プロモーションを含む場合があります

SymPyは、Pythonで数式計算を行うためのライブラリです。
方程式を解いたり、微分積分を行ったり、行列を扱ったりすることができます。
この記事ではSymPyの使い方の紹介と簡単なチュートリアルを行い、最後に微分方程式を解いてみます。

[rotc_mokuji]

Contents

SymPyのセットアップ
SymPyの基本操作
まとめ

SymPyのセットアップ

まず、SymPyをインストールします。pip を使ってインストールすることができます。

pip install sympy

pip install sympy

Jupyter Notebookを使用すると、対話的に実行できるのでおすすめです。
ちなみに、Jupyterは以下のようにpip でインストールすることができます。

pip install jupyter

pip install jupyter

インストールが終了したら、作業フォルダに移動してから以下のコマンドでJupyter Notebookを起動します。

cd <作業フォルダ>
jupyter notebook

cd <作業フォルダ>
jupyter notebook

するとブラウザが起動し、以下のようなJupyterの画面が出ます。
右上のNewボタンでファイルを新規作成しておきましょう。

SymPyの基本操作

記号の定義

SymPyで記号計算を行うには、まず計算に使う文字を「記号」として定義する必要があります。symbols() 関数を使って定義します。

import sympy

# x, y, zを記号として定義
x, y, z = sympy.symbols('x y z')

import sympy

# x, y, zを記号として定義
x, y, z = sympy.symbols('x y z')

また、定義した文字が何者なのか（実数／複素数、正負などを指定することもできます。）

# t 記号として定義。t>=0 を仮定。
t = sympy.symbols('t', nonnegative=True)

# t 記号として定義。t>=0 を仮定。
t = sympy.symbols('t', nonnegative=True)

条件の指定方法は以下の公式ページに記載されています。
Assumptions – SymPy 1.14.0 documentation

式変形

記号を定義すれば、通常のPythonの演算子を使って数式を組み立てることができます。

expr = x + 2*y
print(expr)  # 出力: x + 2*y

# 展開
expanded_expr = (x + y)**2
print(expanded_expr.expand())  # 出力: x**2 + 2*x*y + y**2

# 因数分解
factored_expr = x**2 - y**2
print(factored_expr.factor())  # 出力: (x - y)*(x + y)

expr = x + 2*y
print(expr)  # 出力: x + 2*y

# 展開
expanded_expr = (x + y)**2
print(expanded_expr.expand())  # 出力: x**2 + 2*x*y + y**2

# 因数分解
factored_expr = x**2 - y**2
print(factored_expr.factor())  # 出力: (x - y)*(x + y)

式の出力方法 3選

えりるさんが良く使う数式の出力方法をは以下の３つです。

Pythonコードでそのまま貼り付けることができる形式
LaTeX数式記法
数式そのまま

import sympy

expr = (x + 2*y/z) * sympy.exp(t)

# Pythonコードでそのまま貼り付けることができる形式
print(expr) # 出力: (x + 2*y/z)*exp(t)

#  LaTeX数式記法
print(sympy.latex(expr)) # 出力: \left(x + \frac{2 y}{z}\right) e^{t}

# 数式そのまま
# 出力するにはJupyterのコードブロックの一番下に変数をそのまま記述します。
expr

import sympy

expr = (x + 2*y/z) * sympy.exp(t)

# Pythonコードでそのまま貼り付けることができる形式
print(expr) # 出力: (x + 2*y/z)*exp(t)

#  LaTeX数式記法
print(sympy.latex(expr)) # 出力: \left(x + \frac{2 y}{z}\right) e^{t}

# 数式そのまま
# 出力するにはJupyterのコードブロックの一番下に変数をそのまま記述します。
expr

数式そのままの場合は以下のように、数学の記法（なんて言うんだろ？）で出力されます。

えりる

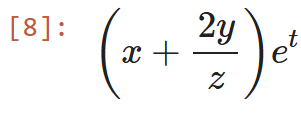
めっちゃ見やすいのでおすすめ！

方程式を解く

SymPyで方程式を解くには、solve() 関数を使います。solve() は、与えられた式がゼロに等しいという前提で、その式を解きます。solve() は、辞書形式で解を返します。

では実際に等式を解いてみましょう。
例えば、$$x + 5 = 0$$ という方程式を解く場合、式を x + 5 と表現します。

import sympy

# 等式の定義
x = sympy.symbols('x')
equation = x + 5

# 式を解く
solution = sympy.solve(equation, x)

print(solution)  # 出力: [-5]

import sympy

# 等式の定義
x = sympy.symbols('x')
equation = x + 5

# 式を解く
solution = sympy.solve(equation, x)

print(solution)  # 出力: [-5]

複数の変数を持つ方程式や、連立方程式も解くことができます。

import sympy

x, y = sympy.symbols('x y')
eq1 = x + y - 10
eq2 = 2*x - y - 5

solutions = sympy.solve((eq1, eq2), (x, y))
solutions  # 出力: {x: 5, y: 5}

import sympy

x, y = sympy.symbols('x y')
eq1 = x + y - 10
eq2 = 2*x - y - 5

solutions = sympy.solve((eq1, eq2), (x, y))
solutions  # 出力: {x: 5, y: 5}

微分と積分

SymPyでは、微分は diff()、積分は integrate() を使って行います。

微分

diff(式, 変数) の形式で使います。

import sympy

x = sympy.symbols('x')
f_x = sympy.cos(x)
derivative = sympy.diff(f_x, x)
derivative  # 出力: -sin(x)

import sympy

x = sympy.symbols('x')
f_x = sympy.cos(x)
derivative = sympy.diff(f_x, x)
derivative  # 出力: -sin(x)

積分

定積分を求める場合は integrate(式, 変数) の形式で使います。

import sympy

x = sympy.symbols('x')
f_x = sympy.exp(x)
integral = sympy.integrate(f_x, x)
print(integral)  # 出力: exp(x)

import sympy

x = sympy.symbols('x')
f_x = sympy.exp(x)
integral = sympy.integrate(f_x, x)
print(integral)  # 出力: exp(x)

定積分を求める場合は、integrate(式, (変数, 下限, 上限)) の形式で使います。

import sympy

x = sympy.symbols('x')
# sin(x) を 0 から π まで積分
definite_integral = sympy.integrate(sympy.sin(x), (x, 0, sympy.pi))
definite_integral # 出力: 2

import sympy

x = sympy.symbols('x')
# sin(x) を 0 から π まで積分
definite_integral = sympy.integrate(sympy.sin(x), (x, 0, sympy.pi))
definite_integral # 出力: 2

えりるさんの数学テクニック

今の積分は以下の積分を解いたものです。$$\int_{0}^{\pi} {\sin{x}}\ \mathrm{d}x =2$$
答えは2 になるんですけど、これは$$\sin{x}$$のグラフの山１つ分の面積が２といいうことを意味しています。
この積分はとてもよく出てくるので覚えておくと何かと便利なのでおすすめです。

えりる

sin(x) ひと山２！
覚えておくと積分計算早くなるよ。

微分方程式を解いてみよう

SymPyを使って微分方程式を解いてみましょう。SymPyのdsolve()関数を使って解きます。

単なる微分方程式を解いても面白くないので、運動方程式を解いて物理現象を扱ってみましょうか。
例として、空気抵抗のある自由落下を考えます。
質量を $m$、重力加速度を $g$、速度を $v(t)$ とします。空気抵抗力は速度に比例するとし、比例定数を$k$ とします。

このときの運動方程式は、以下の微分方程式で与えられます。

$$
m\dfrac{\mathrm{d}v}{\mathrm{d}t}=mg−kv
$$

この微分方程式を解いて、速度 $v(t)$ を求めてみましょう。
まずは微分方程式を定義します。

import sympy

# 記号の定義
t, m, g, k = sympy.symbols('t m g k')

# 速度 v は t の関数として定義
v = sympy.Function('v')

# 微分方程式を定義: m * dv/dt = mg - k*v
ode = sympy.Eq(m * v(t).diff(t), m * g - k * v(t))
ode

import sympy

# 記号の定義
t, m, g, k = sympy.symbols('t m g k')

# 速度 v は t の関数として定義
v = sympy.Function('v')

# 微分方程式を定義: m * dv/dt = mg - k*v
ode = sympy.Eq(m * v(t).diff(t), m * g - k * v(t))
ode

定義ができたらdsolveを使って解きます。

# 微分方程式を解く
solution = sympy.dsolve(ode, v(t))
solution

# 微分方程式を解く
solution = sympy.dsolve(ode, v(t))
solution

すると、以下の出力が得られ、微分方程式を解くことができます。ここで、$C_1$ は積分定数です。$$v(t) = C_1 e^{-\frac{k}{m}t} + \dfrac{mg}{k}$$

ちなみに、初期条件（例えば、時刻$t=0$ で速度 $v=0$）があれば、この積分定数を決定することができます。

まとめ

この記事ではPythonで数式計算を行うためのライブラリであるSymPyを紹介しました。
簡単なチュートリアルを行い、最後に微分方程式を解いてみましたがいかがでしょうか。

この手の数式計算を行うソフトウェアで有名なものにMapleがありますが、あれは個人利用だと年間305ドル、学生なら年間75ドルします。
（参考: Maplesoft Store）
Mapleは数式計算のほかにも可視化などいろんな機能がついているのですが、数式計算だけならSymPyで十分だと思いました。

個人で数学や物理の勉強がしたい方や受験などで数学を勉強したい方におすすめです。

えりるさんが気になっている商品紹介コーナー

UGREENの巻き取り式USB-C充電ケーブルです。巻き取り式のケーブルで100WのPD充電できるのが良いポイント。コンパクトなので持ち運びにも室内用、車内用にも便利ですし、100Wいけるので充電器を選べばスマホからノートパソコンまでなんでも充電できます。
ケーブル長さは36/60/82/100cmの4段階調整なので好きな位置で止められないのは注意ですが、ケーブルを束ねたりして管理するのはめんどくさいですし、それから解放されると考えるとえりるさん的にはかなり魅力的ですね(笑)